"Pseudoknots: RNA Structures with Diverse Functions", by D. W. Staple, S. E. Butcher, Public Library of Science Biology (PLoS Biology), June 2005, 3, 6, 956 - 959
Pseudoknots are explained very well diagrammatically using SARS-CoV (Severe Acute Respiratory Syndrome Coronavirus). Specific examples given for pseudoknots for HDV (Hepatitus Delta Virus); DA-R (Diels-Alder reaction); hTR (human Telomerase reverse transcriptase) with an RNA triple-helix; MMTV (Mouse Mammary Tumor Virus) with a frameshift-inducing pseudoknot; PEMV-1 (Pea enation Mosaic Virus) which does a –1 frameshift between genes P1 and P2; and SRV-1 (Simian Retrovirus 1) which also does a frameshift.
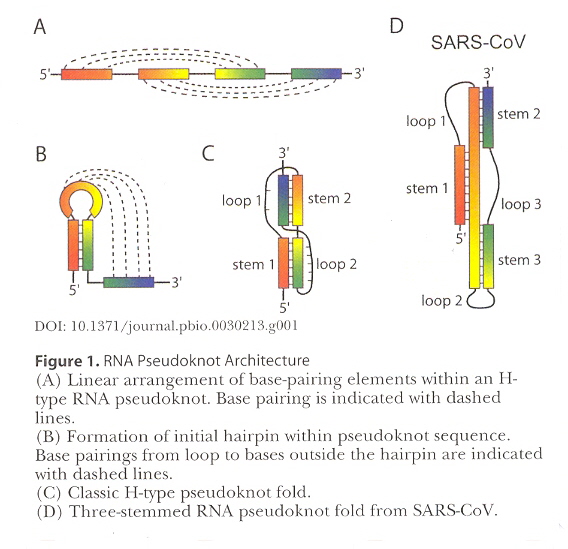
Courtesy of DOI:10.1371/journal.pbio.0030213.g001
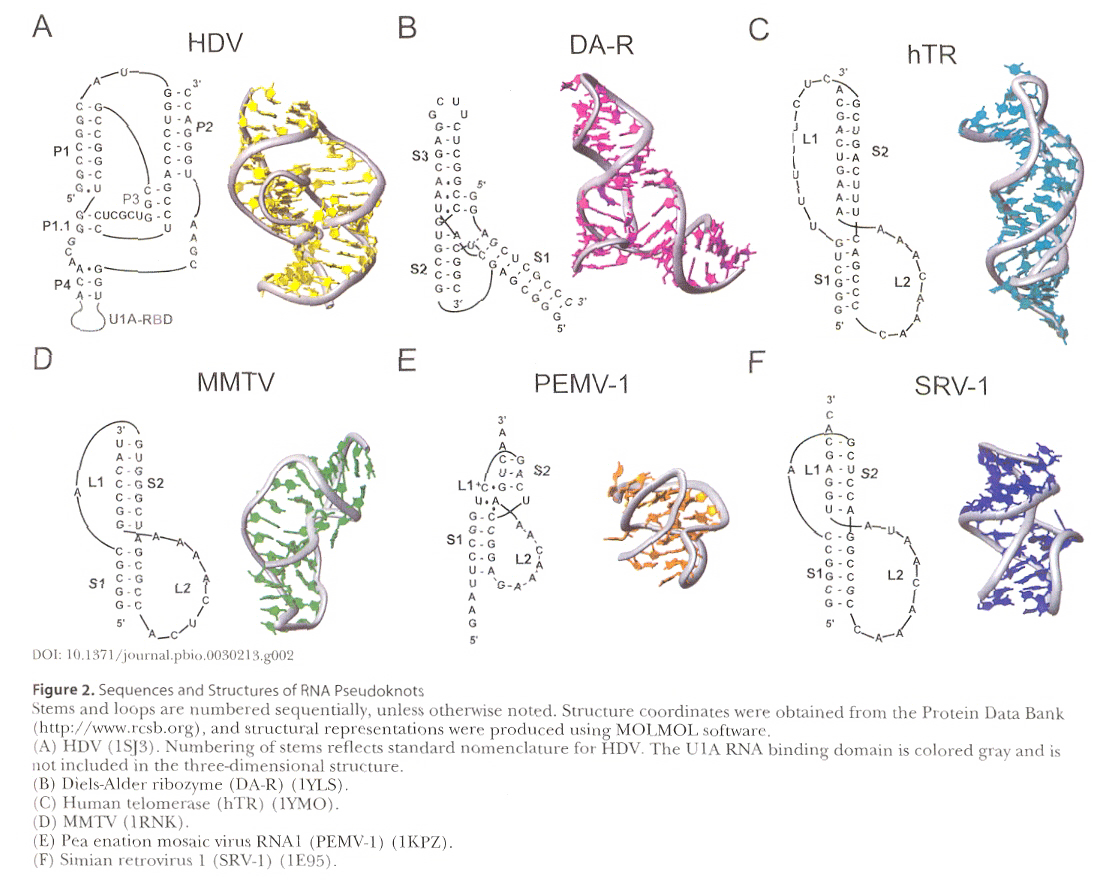
Courtesy of DOI:10.1371/journal.pbio.0030213.g002
"Torsional restraint: a new twist on frameshifting pseudoknots", by E. P. Plant, J. D. Dinman, Nucleic Acids Research, 2005, 33, 6, 1825 - 1833
mRNA pseudo knots stimulate –1 ribosomal frameshifting (&ndash1 PRF). How does a pseudoknot dynamic positioning in the ribosome affect frameshifting? A torsional restraint model suggests that mRNA pseudoknots cause the ribosome to pause with the upstream heptameric slippery site positioned at the ribosomal A- and P-decoding sites. Experiments with a series of pseudo-pseudoknots with different degrees of freedpm are used to test this hypothesis and these experiments support the hypothesis. The heptameric slippry sites ate of the form N NNW WWH (grouping is to show unshifted frames) and where the three N's are identical nucleotides, W are any three A or U nucleotides, and H is A, C, or U. The heptameric site is followed by a spacer region, then the RNA pseudoknot.
Helpful References
Upon encountering the mRNA pseudoknot, sm elongating ribosome is forced to pause so that the anticodons at the ribosomal A snd P site tRNAs are base paired with the zero-frame shifted codons of the slippery site. A relative slip of –1 nucleotide still allows base-pairing in non-wobble positions. Slippage takes place during the ribosomal pause (note; changes affecting ribosomal pause times affect frameshift efficiencies).
The mechanism suggested is that rather than the entire ribosome having to slip one base, slippage can be accomplished by moving a small section of mRNA by one baee in the 31 direction. This is accomplished by the bulky mRNA pseudoknot that is difficult to unwind as the pseudoknot becomes wedged in the downstream entrance into the ribosomal tunnel. This wedging action prevents the downstream mRNA being pulled into the ribosome by the equivalent of one base during elongation, This blockage introduces tension into the downstream spacer region, resloved by unpairing the mRNA from the tRNAs thereby allowing the mRNA to slip backwards by a single nucleotide. The overall result is a net frameshift of one frame by –1 base.
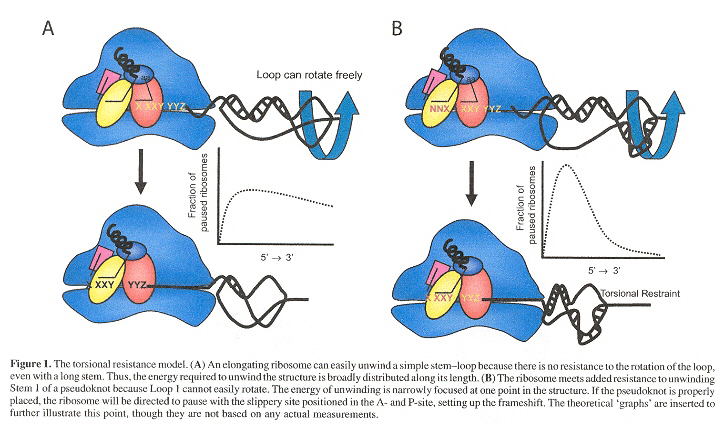
When a stem-loop is unwound by an elongating ribosome, unwinding of the stem forces the loop to rotate. As a simple stem-loop is not restrained, the loop can frely rotate. As a consequence, the potential energy of unwinding is distributed along the lenth of the stem (see Fifure 1A, below). However, if the loop is anchored or restrained (as in a pseudoknot's second stem), stem 1 cannot be fully unwound until stem 2 is first denatured. As the ribosome begins to unwind stem 1, stem 2 forces supercoiling on the remainder of stem 1 therby increasing resistance to ribosomal movement. At some point, the resistance to ribosomal movement due to supercoiling counteracts the forward movement of the ribosome, increasing the probability that the ribosome will pause at a precise point along the mRNA. As the full unwinding of stem 1 depends upon complete denaturation of stem 2, the potential energy of unwinding the pseudoknot is similarly directed to a specific point. If these pause points occur with tRNAs at ribosomal A- and P-sites positioned at the slippery site, frameshifting is stimulated (see Figure 1B, below). Experimental evidence for this interpretation includes replacing bulges in stem 1 with base pairs, thus increasing the energy required to unwind the first three bases, and an increased ribosomal pause at the slippery site, thus increasing –1 frameshifting. This model eliminates the need for a pseudoknot recognizing factor, the evidence of which has not been forthcoming.
Pseudoknot Torsional Resistance Model of Frameshifting
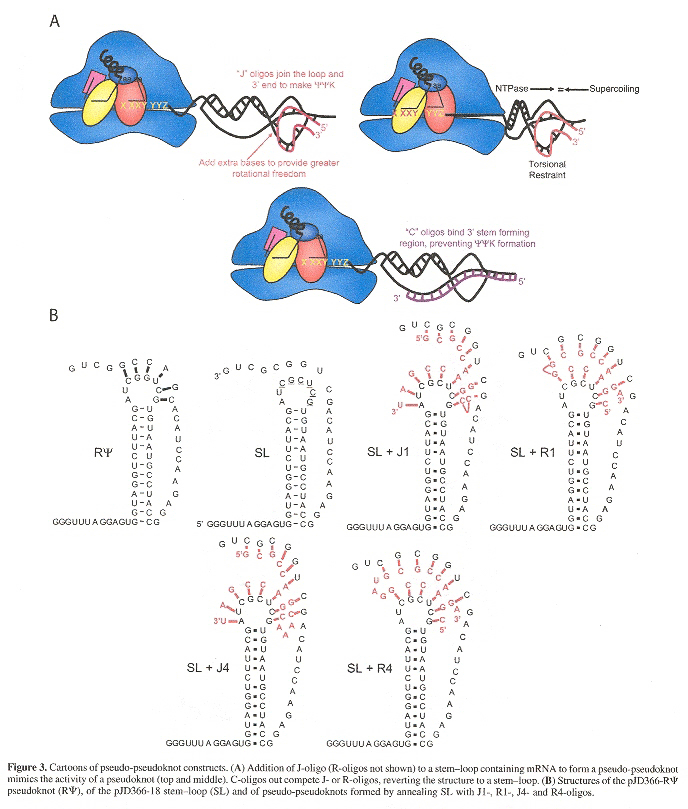
Pseudo-pseudoknot structures have been used to test this pseudoknot torsional resistance model to explain frameshifting at the ribosomal site. This experimental evidence is consistent with the hypothesis described.
Pseudo-pseudoknots used to test the Hypothetical Model
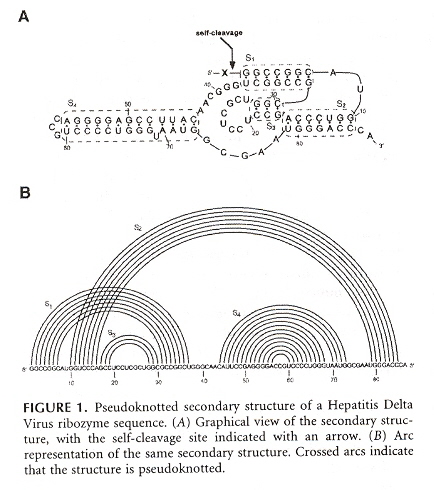
"HotKnots: Heuristic prediction of RNA secondary structures including pseudoknots", by J. Ren, B. Rastegari, A. Condon, H. H. Hoos, RNA, Oct. 2005, 11, 10, 1494 - 1504
What is of greatest significance in this paper is the pattern of a pseudoknot in a Nussinov plot. To be explicit, a pseudoknot is indicated by the presence of crossing arcs or intersecting Nussinov flowers. In "Emergent Computation: Emphasizing Bioinformatics", a single intersecting arc was used to explain tertiary folding, but when there are a number of arcs in the pattern of intersecting flowers, then this identifies a pseudoknot. In the figure below, also note the bulge at position 69 and how it affects the corresponding flower.
"Dynamic programming algorithms for RNA secondary structure prediction with pseudoknots", by T. Akutsu, Discrete Applied Mathematics, 2000, 104, 45 - 62
This paper very nicely describes pseudoknot chains, and provides an O(n4–δ) where n is the number of base pairs, and a dynamic programming algorithm that supports RNA folding including pseudoknots.
|
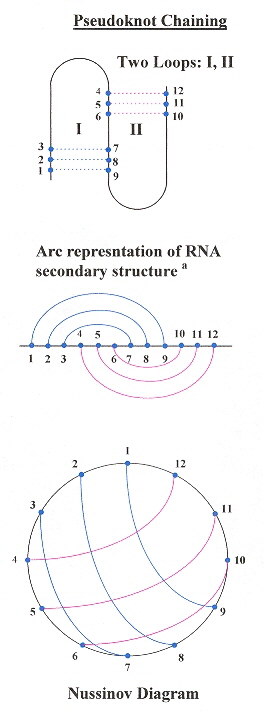
Two-Loop Pseudoknot Chain
|
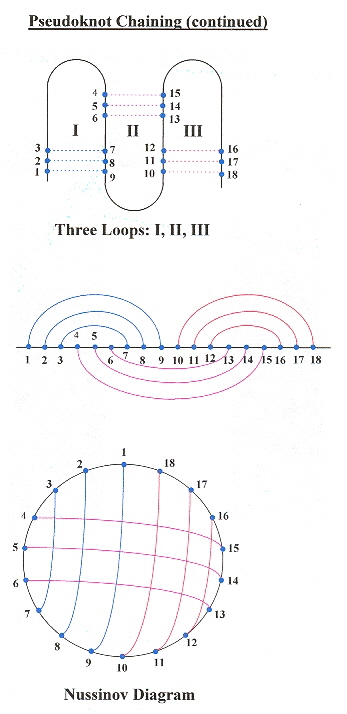
Three-Loop Pseudoknot Chain
|
Four-Loop Pseudoknot Chain
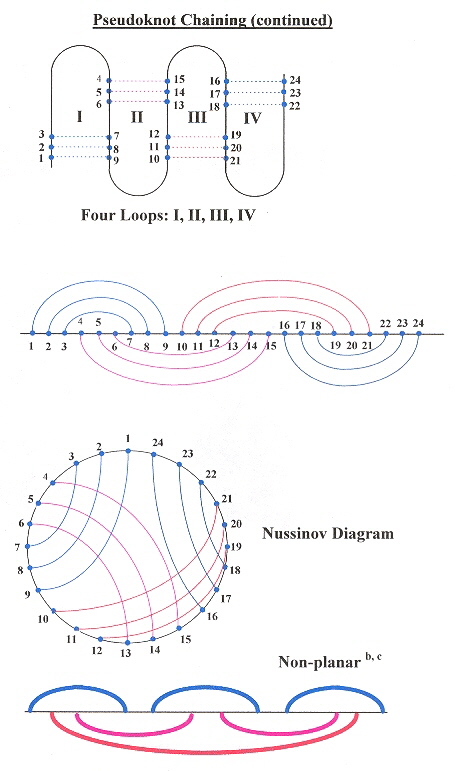
Rivas and Eddy b propose a new kind of context-free grammar: G = ( VN, VT, S, VI, P, R), where:
- VN are non-terminal symbols
- VT are terminal symbols, and include the empty string &lambda, and the hole string ∧ of length zero, or |∧| = 0
- S ∈ VN, the designated start symbol or axiom
- VI are special non-terminal symbols that may only appear on the right of a production rule.
- P is a finite set of prpduction rules
- R a finite set of rearrangement rules that apply after production rule P have been applied and all conventional non-terminals have been eliminated.
Eddy & Rivas b Pseudoknot Grammar
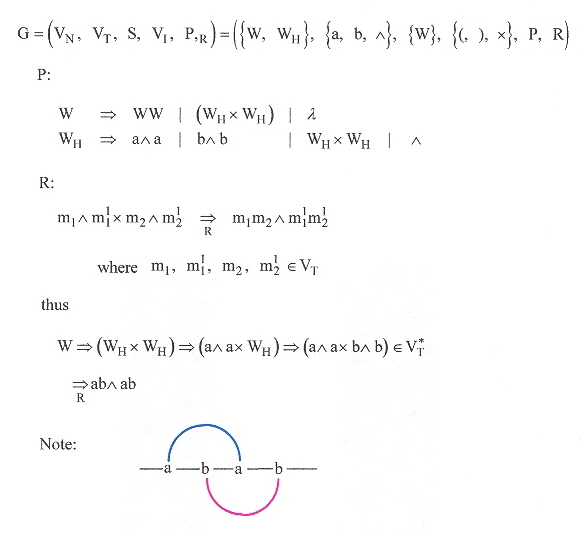
a "Classifying RNA pseudoknotted structures", by A. Condon, B. Davy, B. Rastegari, S. Zhao, F. Tarrant, Theoretical Computer Science, 2004, 320, 35 - 50
b "The language of RNA: a formal grammar that includes pseudoknots", by E. Rivas, S. R. Eddy, Bioinformatics, 2000, 16, 4, 334 - 340
c "RNA Pseudoknot Prediction in Energy-Based Models", by R. B. Lyngsø, C. N. S. Pedersen, Journal of Computational Biology, 2000, 7, 3-4, 409 - 427
"Cap-independent Translation of Tobacco Etch Virus is Conferred by an RNA Pseudoknot in the 5'-Leader", by V. Zeenko, D. R. Gallie, The Journal of Biological Chemistry, July 22, 2005, 280, 29, 26813 - 26824
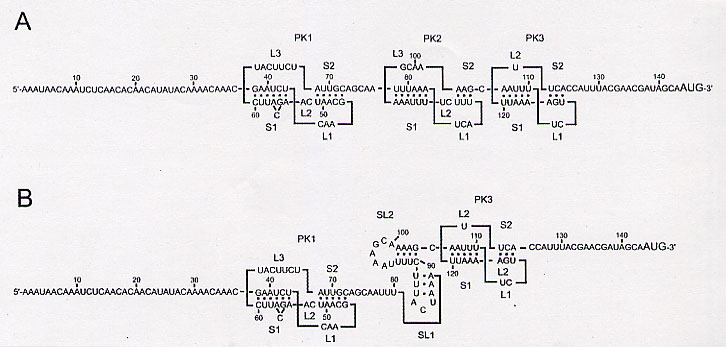
The point of interest is that three pseudoknots labeled PK1, PK2, and PK3 are of central importance in this paper.
PK1 is an H-type pseudoknot with two stems, S1 (6 bp) and S2 (5 bp), that are connected by loops L1 (3 nt), L2 (2 nt), and L3 (7 nt) Fig. 2A). S1 contains a 1-base bulge at C56. S1 and S2 are separated by two nucleotides of L2 at C52 and A53. PK1 is flanked by a 5'-proximal 37-nt sequence with little secondary structure.
PK2 is an H-type pseudoknot with two stems, S1 (6 bp) and S2 (3 bp), that are connected by loops L1 (3 nt), L2 (2 nt), and L3 (4 nt) Fig. 2A). S1 and S2 are separated by two nucleotides of L2 at C90 and U91. An alternative structure to PK2 is composed of two stem-loops (Fig. 2B).
PK3 is an H-type pseudoknot with two stems, S1 (5 bp) and S2 (3 bp), that are connected by loops L1 (2 nt), L2 (1 nt), and L3 (7 nt) Fig. 2A).
"Functional analysis of the pseudoknot structure in human telomerase RNA", by J-L. Chen, C. W. Greider, Proceedings of the National Academy of Sciences U.S., June 7 2005, 102, 23, 8080 - 8085
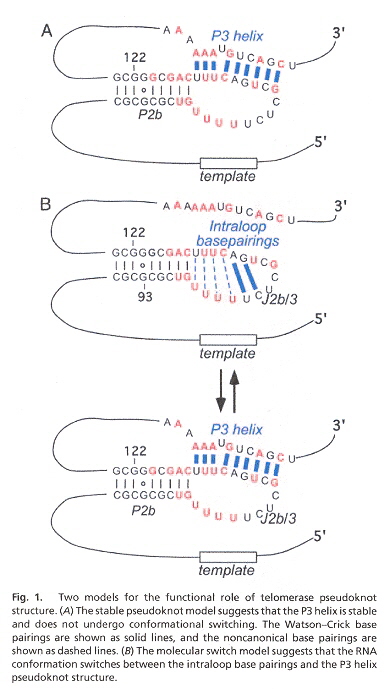
RNA provides a template for telomeric repeat synthesis and pseudoknots are conserved in ciliates and vertibrates. Thus study uses mutations in which intra-molecular vs inter-molecular switching (at helix P3) can be examined. The authors conclude that pseudoknots do not act as a switch (in this particular case of telomeres). However, switching activity of pseudoknots may well exist in other cases of telomeres or non-telomers. This study most clearly explains the thesis of pseudoknot switching, however.
Telomerase RNA (TR) has helix structures at P2b, J2b/3, and P3 (see the figure, below). Switching can take place between helix P3 and J2b/3.
|
TR Pseudoknot Switching
|
Intra-molecular vs Inter-molecular Switching
|
"Asymmetry in RNA pseudoknots: observation and theory", by D. P. Aalberts, N. O. Hodas, Nucleic Acids Research, 2005, 33, 7, 2210 - 2214
RNA pseudoknots are composed of a secondary structure that can be depicted as nested blocks of non-nested dsRNA mixed with base pairs composed of helices, bulges, and hairpins joined with ssRNA loops. Common examples of nested secondary motifs include:
- AABB
- ABBA
- ABAB
- ABACBC
- ABACCB

The authors of this paper point out that the population of RNA bases in stems and loops vary, and few pseudoknot algorithms and models can explain these statistics. The authors feel that known pseudoknots should be examined, such as those in oBase . The authors attempt a study of RNA pseudoknots from the viewpoint of polymer physics and statistical mechanics. As an example of their approach, the ABAB motif is examined with the following mathemmatical approach (similar methods for other motifs). See:


What follows are a series of papers which are of a more mathematical nature, but which are of great significance with regards to language theory. Specifically, these papers are useful when dealing with secondary RNA structures, including pseudoknots.
Trees can be modified, and in this respect, there are three kinds of modifications that are of the greatest importance. These modifications are important in changing or editing trees from one form to another (due to errors, or reallignments, etc.) a. These operations are applied to ordered trees in preorder traversal (verticies are visited in the order left to right). An ordered tree is a tree in which the order of the subtree is signiificant. Thus vertex A with subvertices B then C is different than vertex A with subvertices C then B. It should be noted that the following three operations constitute the Damerau–Levenshtein metric c, d for error–correction or editing (substitution, deletion, insertion).
- Vertex B changed to vertex C, or in short hand: B → C
- Vertex B is deleted (along with any edge to B), and the subtree at B is attached to the vertex that originally connected to B, or in shorthand: B → λ
- Vertex C is attached to a vertex, and and subtree at that vertex is attached to vertex C, or in shorthand: λ → C
Tree-editing Operations
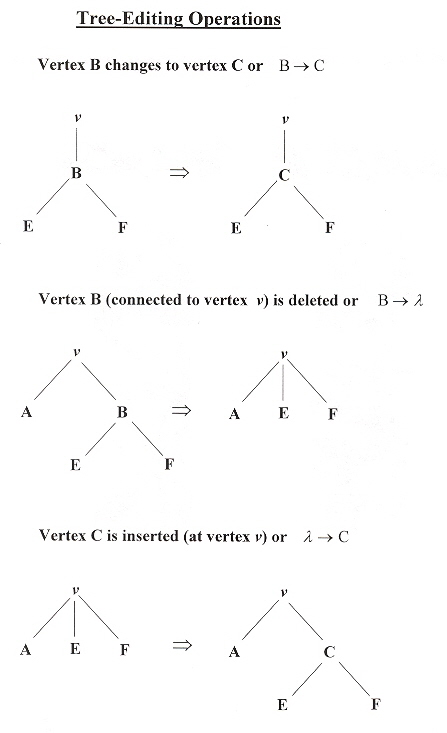
It is then possible to create a mapping between two trees T, and T1, associating verticies.
- A dotted line between verticies shows how verticies change
- Verticies in T not touched by a dotted line are deleted
- Verticies in T1 not on a dotted edge are inserted
Tree Mapping

While other usefull theorems are in this paper, let us resume our specific interest and keep our eyes on languages for RNA with pseudoknots.
We resume with pair hidden Markov models (PHMM), applied to tree structures, and specifically, pair hidden Markov models applied to stochastic tree automata or PHMMTS b.
Stochastic Tree Automata

PHMMTS

The previous methods developed by Y. Sakakibara in combination with K-C. Tai are not of sufficient power to deal with pseudoknots, but this section will discuss continuing developments that are sufficiently powerful to support pseudoknots e.
Tree Adjoinung Grammars (TAGs) are a subclass of context-sensitive grammars of sufficient power to support secondary RNA folding including pseudoknots. What is proposed are Pair Stochastic TAGs (PSTAGs). Instead of using PHMMTSs defined on aligned trees, PSTAGs are used to align "TAG trees", along with a dynamic programming parser for TAGs. Two special subclasses of TAGS developed by Uemura f are used:
- Simple linear TAGs (SL-TAGs)
- Extended simple linear TAGS (ESL-TAGs)

Now for the SL-TAGs and ESL-TAGs of Uemura. An initial tree tinitial is simple linear if tadjunct has exactly one active vertex on its backbone. In this situation, a TAG G is a simple linear TAG if all elementary trees in G aresimple linear. An adjunct tree tadjunct is semi-simple linear if tadjunct has exactly two active vertices where one is on its backbone and the other is not on the backbone. A TAG G is an extended simple linear TAG if initial trees in G are simple linear and all djunct trees in G are either simple linear or semi-simple linear. Consider the following decomposition.
Decomposition
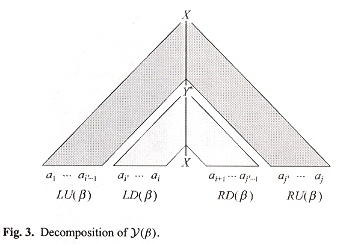
ESL-TAGs

Pseudoknot RNA ESL-TAGs
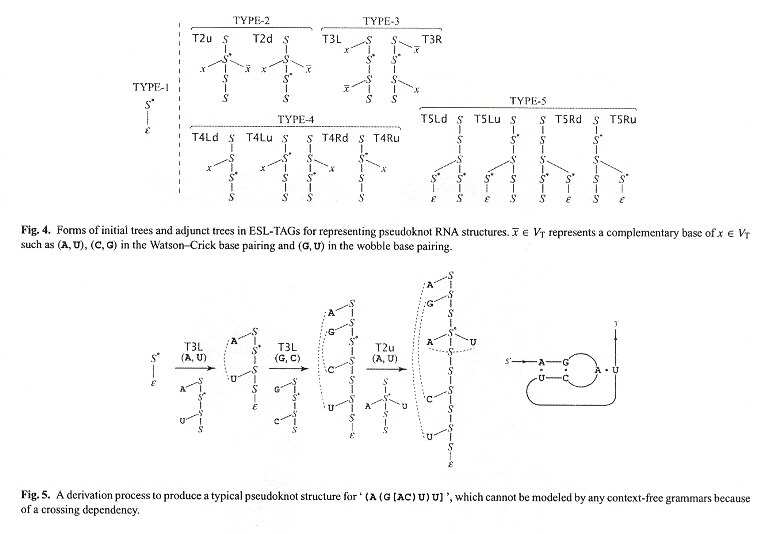
PSTAG
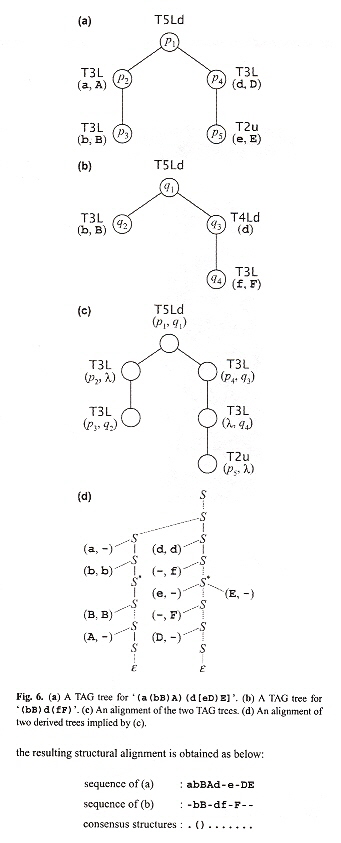
Effectively, this algorithm combines tree mapping with Stochastic TAG trees with CYK parsing and produces RNA secondary structures that can contain pseudoknots as in the figure below.
PSTAG RNA
a "The Tree-to-Tree Correction Problem", by K-C. Tai, Journal of the Association for Computing Machinery, July 29 1979, 26, 3, 422 - 433
b "Pair hidden Markov models on tree structures", by Y. Sakakibara, Bioinformatics, 6/29/2003 - 7/3/2003, 19, Suppl. 1, Eleventh International Conference on Intelligent Systems, for Molecular Biology, Brisbane, Australia, i232 - i240
c "Binary Codes Capable of Correcting Deletions, Insertions, and Reversals", by V. I. Levenstein, 1966, Soviet Physics Doklady, 10, 8, 707 - 710
d "A Techniqwue for Computer Detection and Correction of Spelling Errors", by F. L. Damerau, 1964, Communications of the Association for Computing Machinery, 7, 3, 171 - 176
e "Sequence analysis Pair stochastic tree adjoining grammars for aligning and predicting pseudoknot RNA structures", by H. Matsui, K. Sato, Y. Sakakibara, Bioinformatics, June 1 2005, 21, 11, 2611 - 2617
f "Tree adjoining grammars for RNA structure prediction", by Y. Uemura,A. Hasegawa, S. Kobayashi, T. Yokomori, Theoretical Computer Science, 1999, 210, 277 - 303
"Simple fast algorithms for editing the distance between trees and related problems", by K. Zhang, D. Sasha, SIAM Journal of Computing, 1989, 18, 1245 - 1262
"A grammar-based unification of several alignment and folding algorithms", by F. Lefebvre, Proceedings of the 4th International Conference on Intelligent Systems for Molecular Biology, 1996, 143 - 154
"Automata-Theoretic Models of Mutation and Alignment", by D. B. Searls, K. P. Murphy, Proceedings of the 3rd International Conference on Intelligent Systems for Molecular Biology, 1995, 341 - 349
"The language of RNA: a formal grammar that includes pseudoknots", by E. Rivas, S. R. Eddy, Bioinformatics, 2000, 16, 4, 334 - 340
"A Partition Function Algorithm for Nucleic Acid Secondary Structure, Including Pseudoknots", by R. M. Dirks, N. A. Pierce, Journal of Computational Chemistry, Oct. 13 2003, 24, 1664 - 1677